[
In Antwort auf #49252]
Hallo Steffen,
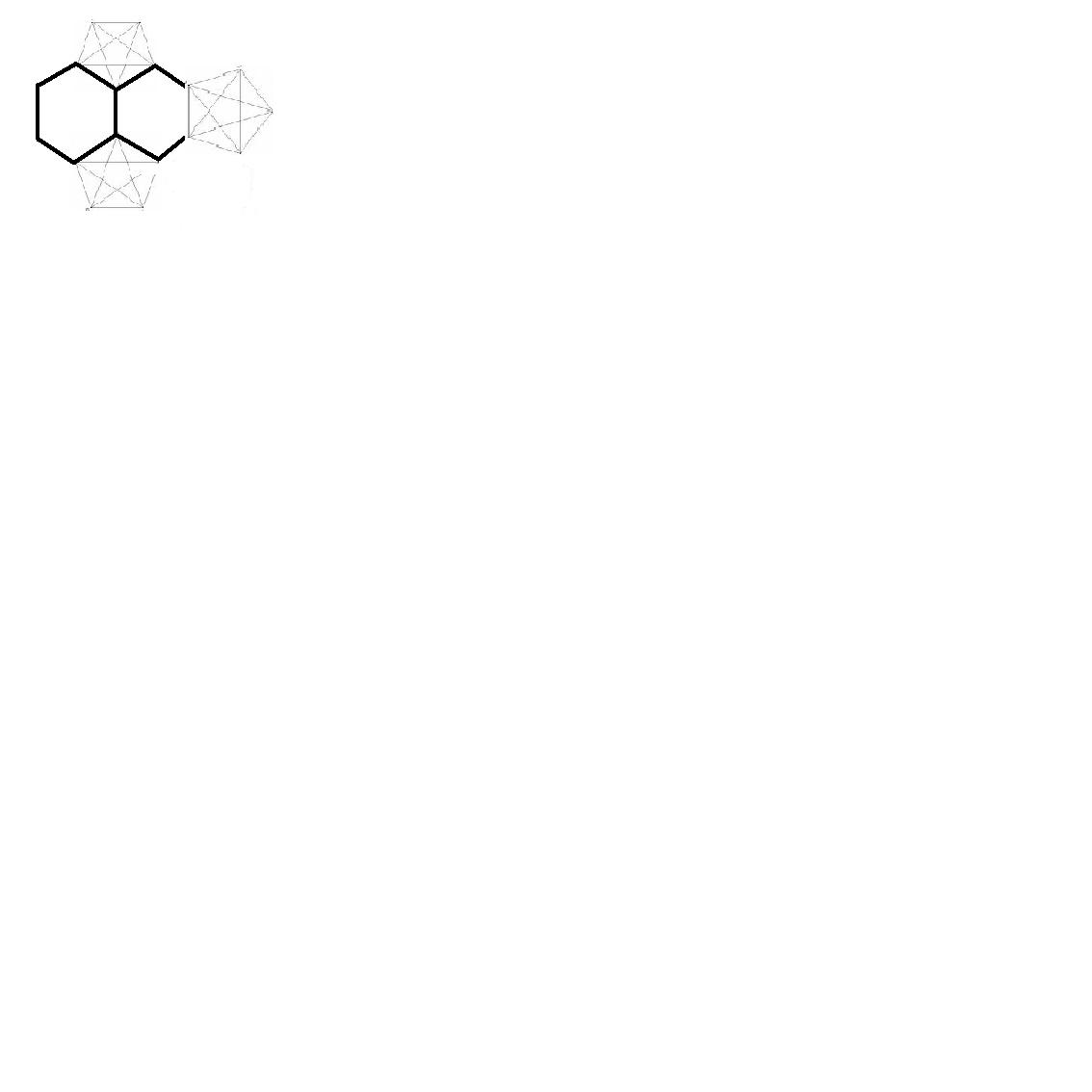
für Dein 'Fußballbett' brauchst Du 20 regelmäßige Sechsecke und 12 regelmäßige Fünfecke. Mit diesen regelmäßigen Vielecken (Polygone) kannst Du die Kugel (Ball) nachbauen (genauer: der Kugel annähern).
Einen guten Überblick (Video) kannst Du Dir hier verschaffen (Link1):
http://www.br-online.de/wissen/forschung/fussball-forschung-DID1211190251232/index.xmlhier: Mathematik zum Anfassen: Der Fussball
( Sehr anschaulich, keine Formeln!)
Ein Netz Deines Fußballs findest Du hier (Link2):
http://www.korthalsaltes.com/index.htmlhier:
Truncated lcosahedron (soccer ball)
Dieses Netz - in 6 Teilnetze aufgeteilt - gibt es hier:
pdf version
Zum Problem:
Wie lang ist die Seitenkante eines Sechs- bzw. Fünfecks zu wählen?
Die regelmäßigen Sechsecke (Hexagon) und regelmäßigen Fünfecke (Pentagon) haben alle die gleichen Kantenlänge.
Berechnung der Seitenkante a:
1. Die Fläche eines regelmäßigen Sechseckes: A = a^2 / 4 * √3
2. Die Fläche eines regelmäßigen Fünfecks: A = 5/4 * a^2 * tan(54°)
3. Die Oberfläche der Kugel: O = 4 * pi * r^2
4. Der Radius der Kugel wäre die Hälfte Deiner Bettlänge, also etwa 85cm
Ansatz:
Oberfläche Kugel >= 20*Fläche Sechseck + 12*Fläche Fünfeck
4 * pi * r^2 >= a^2*(5*√3 + 15*tan(54°))
Wenn ich mich nicht verrechnet habe, ergibt sich:
Formel: 0,82*r >= a
Steffen, hier ist meine Lösung:
Bei einem Durchmesser von 1,70m, also einem Radius von 85 cm, ergibt sich eine Seitenkante von etwa a = 0,82*r,
also r etwa 70 cm (69,7 cm).
Da Du von mindestens 1,70 m Durchmesser gesprochen hast, wähle den Durchmesser 1,80 m. Dann wäre a etwa 75 cm.
Die Anordnung der Vielecke entnimmst Du--> Link2.
Die Formel ist allgemeingültig. Wenn Du erst ein Modell bauen möchtest mit einem Durchmesser
von 10 cm, wählst Du die Seitenkante der Vielecke 8,2 cm.
Steffen Du weißt ' Alle Theorie ist grau'. Jetzt ist der Praktiker gefragt. Ich bin auf Erfahrungen gespannt und hoffe, dass ich Dir auf deinem Weg zu einem 'Fussballbett' (Fussballhaus) für Deine Jungs etwas helfen konnte. Viel Erfolg!
MfG
Hans-Peter